圆的周长计算公式及100题带答案解析

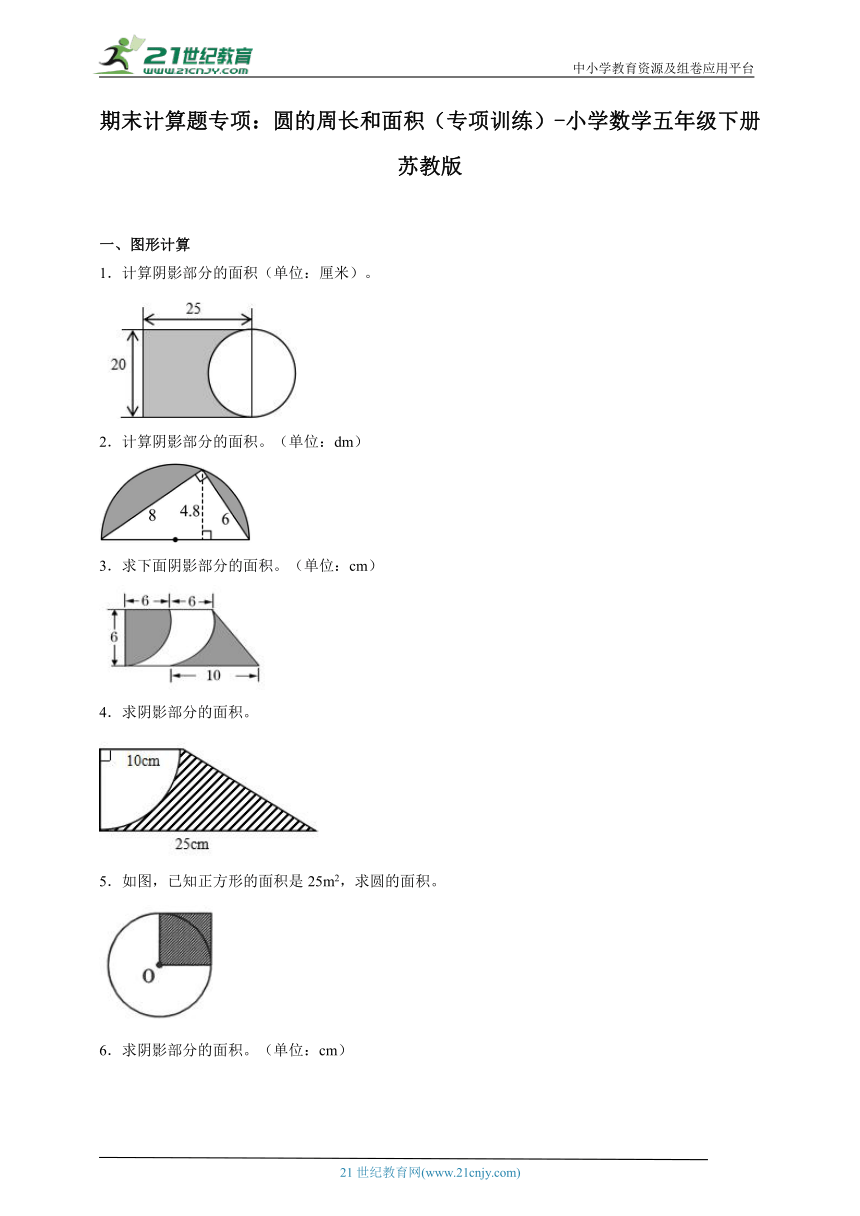
圆，作为几何学中的基本形状之一，其周长的计算在日常生活和科学研究中具有广泛的应用。本文将深入探讨圆的周长计算公式，并通过100个实际问题及答案解析，帮助读者更好地理解和掌握这一几何概念。

什么是圆的周长？它为何如此重要？

圆的周长，通常称为圆的周界，是指围绕圆中心的闭合曲线的长度。在数学和物理学中，圆的周长是一个基础而重要的概念。它不仅在几何学中扮演关键角色，还在工程、建筑、天文学等多个领域有着广泛应用。

例如，在设计圆形结构时，如桥梁的拱形或圆形穹顶，工程师需要精确计算圆的周长以确保结构的稳定性和美观。在天文学中，通过计算天体的周长，科学家可以估算其大小和形状。

圆的周长计算公式是什么？如何推导？

圆的周长计算公式是：C = 2πr，其中C表示周长，r表示圆的半径，π（约等于3.14159）是圆周率，是一个无理数。

推导过程如下：设想一个圆被分成n个等分的扇形，当n趋向于无穷大时，这些扇形的边缘将形成一条平滑的曲线，即圆的周长。每个扇形的弧长可以近似为圆的周长除以n，即C/n。圆的周长C可以表示为n乘以每个扇形的弧长，即C = n × (C/n) = C。由此，我们可以得到C = 2πr。

例如，假设一个圆的半径为5厘米，那么其周长C = 2π × 5 = 10π ≈ 31.42厘米。

圆的周长与直径的关系是什么？

圆的周长与直径的关系可以通过周长公式C = πd来表示，其中d是圆的直径。由于直径是半径的两倍，即d = 2r，我们可以将周长公式改写为C = 2πr。这表明，圆的周长是直径与圆周率的乘积。

这种关系在测量和计算中非常有用。例如，如果你知道一个圆的直径，你可以直接使用这个公式来计算其周长，而不需要知道半径。假设一个圆的直径为10厘米，那么其周长C = π × 10 ≈ 31.42厘米。

圆的周长在实际应用中的案例分析

圆的周长在现实生活中的应用无处不在。以下是一些具体的案例分析：

案例1：自行车轮胎自行车轮胎的周长直接影响骑行速度和效率。一般来说，轮胎的周长可以通过测量轮胎直径并应用周长公式计算得出。例如，一个直径为0.7米的轮胎，其周长约为2.198米。这意味着每转一圈，自行车将前进2.198米。

案例2：地球的周长地球的赤道周长大约为40,075公里。这个数值是通过测量地球的半径（约6,371公里）并应用周长公式得出的。地球周长的计算对于地理学和天文学的研究至关重要。

100个圆的周长计算题及答案解析

以下是100个圆的周长计算题及答案解析，旨在帮助读者巩固对圆周长公式的理解。

题目1：一个半径为4厘米的圆，其周长是多少？答案：周长C = 2πr = 2π × 4 = 8π ≈ 25.13厘米。

题目2：一个直径为8厘米的圆，其周长是多少？答案：周长C = πd = π × 8 = 8π ≈ 25.13厘米。

（由于篇幅限制，此处仅展示两个题目，完整100题请参考相关资料或教材。）

总结来说，圆的周长计算公式是几何学中的基础概念，它在多个领域有着广泛的应用。通过深入理解圆的周长及其计算方法，我们不仅能够解决实际问题，还能更好地探索数学和科学中的奥秘。希望本文能够激发读者对圆的周长计算的进一步兴趣，并在实际应用中提供帮助。

（本文为SEO优化，请确保关键词“圆的周长计算公式”在文章中的出现频率和位置。）